by zhangxinxu from http://www.zhangxinxu.com
本文地址：http://www.zhangxinxu.com/wordpress/?p=3855

一、一剂预防针

好的体验应该是在用户试用之前就告知产品的一些特点、局限性等。类似裤子都脱了，才来一句：“我今天大姨妈巅峰期”的场景显然是会让兴致勃勃的用户受挫的。

SO, 有必要在这里打个预防针，本文实际上没什么技术养料，就是昨晚因实际工作需要折腾的个东西，抛物线轨迹动画。如果你急着跟女神搞昧，下面的可以直接pass~~

不过这里有个有养料的东西，要跟大家分享下，当当当当，就是下面这个：

正宗曲江猕猴桃。公司福利，内部价，37元一箱，对！你没看错！就是37元！货真价实37元！足足有27个猕猴桃！各个多汁甜美，诱人无比！我周围同事几乎人人搞了一箱！是不是超划算哈！是不是很心动啊！是不是很羡慕哈！我厂类似有养料的福利还有很多哦！心动不行动，把妹永被动。偷偷告诉你哦，我们这边还差一个前端，我们ISUX上海可是我厂非常优秀的团队哦，还不简历速速飞来 – zhangxinxu@zhangxinxu.com . 不要担心，你简历再low我也会耐心回复你的，绝对不会石沉大海，重复过去你的不开心经历的哈！

二、动画与视觉引导

在页面上添加元素的位移动画，除了视觉效果（这是次要的），还有个作用就是视觉引导（重点）。举个大家可能见过的例子，选择商品的时候，我们希望商品飞到边缘或角落的购物车里，作用是：一来告知放在购物车里成功了，二来让用户知道购物车在哪里。

但是，直来直去的运动你用我也用，不出彩啊，于是，就有想法，我抛物线过去，会不会有别样的风采。

于是，下班后就抽时间折腾哈~~

于是就有了今天这篇没什么养料的文章。

哈，稍等，我先回家，夫人催了，回去吃个猕猴桃补充下养料，继续哈……

三、数学函数与动画轨迹

//zxx: 翌日……

常有云：“书到用时方恨少”。其实我觉得这有一部分责任在教者身上。好比高中时候，拼死拼活学各种函数曲线。我们为什么而学？很明显，为了考试！短视而功利的教育环境让老师一族的眼界也放在了考试成绩上。这也是为何中国学习应试考试一级棒，实践与创新吊车尾的原因。

实际上，学习这些函数不是为了考试，而是为了日后的工作、解决生活实际问题。知道这些可以做什么，才能培养真正的兴趣，才能真正出类拔萃，学以致用。所以，您不必懊悔当初没好好学习什么的，是大环境限制了你当时的学习。

就拿计算机图形动画举例，实际上，任何有规律的运动都是数学函数的呈现。

试想下，如果数学老师可以把函数，与实际应用结合，比方说告诉喜欢玩游戏的同学：《剑灵》《英雄联盟》中那些绚烂的效果都是这里的抛物线啊重力啊等一干函数实现的。要是你们对游戏感兴趣，从事游戏相关的工作，这些函数是要牢牢掌握的哦！这种教育要比“你不好好学习，考个好成绩，找个好工作”有用多了。如果再能手把手辅导出什么不一样的成果——小装置，或者小游戏之类。我擦，那还不上天了！这个娃未来不是精英也是奇葩！

哈，讲正经的。

要让页面元素抛物线运行，很简单。套用抛物线函数即可。公式如下：

y = a*x*x + b*x + c

(x, y)就是点坐标，在网页上可以理解为相对于页面左上角的偏移像素大小。

然后，套用求参，即可得到当前位置的抛物线函数啦！当然，实际操作不是键盘啪啪几个文字这么简单。

四、抛物线函数求解

//zxx: 如果本段内容勾起你过去那段惨绝人寰的回忆，我这里先说声抱歉！ – 搞咩纳塞~

现在，我们的任务变成了求解：a, b, c三个参数。

3个参数需要3个条件才能完全求解。

由于我们要实现元素A到元素B的抛物线运动，因此，我们可以指定两个点的坐标位置，也就是知道了2个条件，那第3个条件呢？

了解抛物线函数的同学应该知道，a可以近似理解为弧度，曲率。在我们实现效果的时候，这个是应该要可控的。——你总不可能把元素抛到天宫号上再掉下来吧。在网页上，一般都是起伏不大的抛物线（否则会出屏幕之外）。

因此，我们可以把a作为一个参数常量。

于是，我们任务就变成了，已知参数a，以及两个点的坐标，求该抛物线函数。

哈，事情就简单多了。

y = a*x*x + b*x + c
↓
y1 = a * x1*x1 + b*x1 + c;
y2 = a * x2*x2 + b*x2 + c;
↓
a已知，求b, c

为了简化我们的计算求解，以及与我们高中时候的函数坐标匹配，我们可以以移动元素的初始位置作为坐标轴的中心（网页默认的坐标系左上角是中心，x轴向右，y轴向下，与高中的坐标轴不一样）。如下链接对应demo所示。

您可以狠狠地点击这里：元素抛物线运动demo

demo页面中，圆形的小球球就是要运动的元素；椭圆的大便池就是小球球运动的目的地，其默认开始的坐标如下所示：

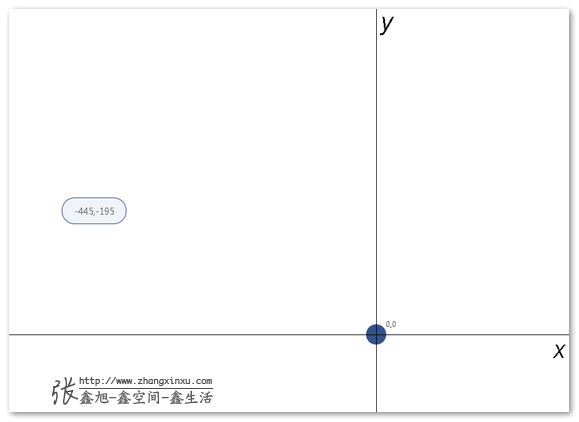
也就是，我们限定了抛物线经过中心点(0, 0), 代入y1 = a * x1*x1 + b*x1 + c可以得到c = 0, 于是b = (y2+ a*x2*x2) / x2, 带入大便池元素的坐标，就可以计算出b的大小，于是，抛物线函数就出来了。

注意，这里“大便池元素的坐标”是相对于小球球的相对坐标，而不是页面左上角。

有了抛物线函数，我们就有了小球球运动的轨迹了。

五、demo演示及说明

demo演示页面就是上面提前曝光的链接地址啦！

1. 点击页面的任意位置，都会触发小球球奔向大便池的抛物线运动。
2. 拖动大便池到页面的任意位置，也会触发小球球义无反顾奔向大便池的效果。

demo页面的这个抛物线运动基本上是个独立的JS方法，代码如下：

var funParabola=function(d,t,g){var i={speed:166.67,curvature:0.001,progress:function(){},complete:function(){}};var p={};g=g||{};for(var v in i){p[v]=g[v]||i[v]}var u={mark:function(){return this},position:function(){return this},move:function(){return this},init:function(){return this}};var e="margin",r=document.createElement("div");if("oninput" in r){["","ms","webkit"].forEach(function(b){var a=b+(b?"T":"t")+"ransform";if(a in r.style){e=a}})}var s=p.curvature,q=0,o=0;var k=true;if(d&&t&&d.nodeType==1&&t.nodeType==1){var n={},j={};var h={},m={};var f={},l={};u.mark=function(){if(k==false){return this}if(typeof f.x=="undefined"){this.position()}d.setAttribute("data-center",[f.x,f.y].join());t.setAttribute("data-center",[l.x,l.y].join());return this};u.position=function(){if(k==false){return this}var b=document.documentElement.scrollLeft||document.body.scrollLeft,a=document.documentElement.scrollTop||document.body.scrollTop;if(e=="margin"){d.style.marginLeft=d.style.marginTop="0px"}else{d.style[e]="translate(0, 0)"}n=d.getBoundingClientRect();j=t.getBoundingClientRect();h={x:n.left+(n.right-n.left)/2+b,y:n.top+(n.bottom-n.top)/2+a};m={x:j.left+(j.right-j.left)/2+b,y:j.top+(j.bottom-j.top)/2+a};f={x:0,y:0};l={x:-1*(h.x-m.x),y:-1*(h.y-m.y)};q=(l.y-s*l.x*l.x)/l.x;return this};u.move=function(){if(k==false){return this}var a=0,b=l.x>0?1:-1;var c=function(){var z=2*s*a+q;a=a+b*Math.sqrt(p.speed/(z*z+1));if((b==1&&a>l.x)||(b==-1&&a<l.x)){a=l.x}var w=a,A=s*w*w+q*w;d.setAttribute("data-center",[Math.round(w),Math.round(A)].join());if(e=="margin"){d.style.marginLeft=w+"px";d.style.marginTop=A+"px"}else{d.style[e]="translate("+[w+"px",A+"px"].join()+")"}if(a!==l.x){p.progress(w,A);window.requestAnimationFrame(c)}else{p.complete();k=true}};window.requestAnimationFrame(c);k=false;return this};u.init=function(){this.position().mark().move()}}return u};(function(){var b=0;var c=["webkit","moz"];for(var a=0;a<c.length&&!window.requestAnimationFrame;++a){window.requestAnimationFrame=window[c[a]+"RequestAnimationFrame"];window.cancelAnimationFrame=window[c[a]+"CancelAnimationFrame"]||window[c[a]+"CancelRequestAnimationFrame"]}if(!window.requestAnimationFrame){window.requestAnimationFrame=function(h,e){var d=new Date().getTime();var f=Math.max(0,16.7-(d-b));var g=window.setTimeout(function(){h(d+f)},f);b=d+f;return g}}if(!window.cancelAnimationFrame){window.cancelAnimationFrame=function(d){clearTimeout(d)}}}());

//zxx: 为节约文章篇幅，这里放的是压缩后的代码。如果您对实现感兴趣，可以demo页面右键的源代码是非压缩版本，含有非常多的注释。或者使用这个JS文件：parabola.js

该抛物线方法名为funParabola，您可以根据自己的喜好修改，参数以及基本使用如下：

var myParabola = funParabola(element, target, options);

关于myParabola:
直接执行funParabola方法是不会产生运动的。因为，实际上funParabola执行返回的是一个对象。包含如下四个方法：

1. mark 在目标元素以及移动元素上通过data-center自定义属性标记当前的中心坐标，如-234, -345. 此方法主要用在demo中，方便测试与预览用的。实际可能用途不大。
2. position 重新获取元素的位置。在元素相对位置改变的时候，此方法很有用。否则会出现计算误差的情况。例如，页面布局是自适应或者响应式的，浏览器宽度变小了，两元素之间的距离变化了，此时需要执行下position，存储新的坐标位置。
3. move 触发抛物线运动。
4. init 初始化方法。实际上就是连续调用position, mark, move3个方法。

demo点击页面任意位置触发抛物线运动就是这么触发的：

/* 元素 */
var element = document.getElementById("element"), 
    target = document.getElementById("target");
// 抛物线元素的的位置标记
var parabola = funParabola(element, target).mark();
// 抛物线运动的触发
document.body.onclick = function() {
    element.style.marginLeft = "0px";
    element.style.marginTop = "0px";
    parabola.init();
};

参数说明：

• element表示移动的元素，例如demo中的小球球。原生DOM节点
• target表示目标元素。例如demo中的椭圆形的大便池。原生DOM节点
• options为可选参数。各个API名称以及含义如下：
  • speed 表示每帧移动的像素大小，每帧（对于大部分显示屏）大约16~17毫秒。默认大小是166.67。也就是默认10px/ms.
  • curvature 可以近似理解为抛物线的开头大小，也就是曲率。正数表示开口向下。默认大小是0.001. 数值越大，开头越小，弧度越高。因为web页面动辄大小几百像素，因此，曲率值较小。
  • progress 表示抛物线运动过程中的回调，支持两个参数，x, y，表示当前的坐标，您可以根据这些坐标值做一些特殊的处理。
  • complete 表示抛物线运动结束后的回调。

其他说明：

1. 可选参数speed不是指x轴的位移，也不是y轴位移，而是抛物线特定坐标的切线距离。利用切线公式：y'=2ax+b就可以计算出x轴这一帧应该移动的距离。形成奔向目的地的运动效果。
2. funParabola方法不依赖任何JS框架。您可以大胆使用。对了，funParabola使用了requestAnimationFrame方法。关于requestAnimationFrame身世、工作等私密信息可以参考我之前的“CSS3动画那么强，requestAnimationFrame还有毛线用？”一文。上面压缩的JS包含了requestAnimationFrame相关的兼容处理，因此IE6浏览器也是可以使用滴！

   如果您使用的是demo源代码中的funParabola方法。如果您想低版本IE浏览器也有效果，需要再调用后面这个JS: requestAnimationFrame.js, 很少量的JS代码，主要做兼容处理的。因此，您可以可以直接拷贝出来。

   当然，最偷懒的方法是直接使用parabola.js或者压缩版parabola-min.js. 建议您拷贝到本地使用，尽量不要直接我站点外链地址。一旦外链请求超过我的忍受程度，我会加上这么一句JS：

   ddocument.body.insertAdjacentHTML("afterBegin", '<a href="ooxxooxxooxxooxx-huluwa.mp4">老板和秘书的激情战斗720x480.mp4</a>');

   大家可以自己斟酌下~

六、实际应用示意

概念作品会让人眼前一亮，但只有实物产品才会让人怦然心动。因此，附上一个符合实际应用场景的例子，即开始提到的“商品飞到购物车”的效果。自然，借助上面折腾的funParabola方法。

您可以狠狠地点击这里：商品抛物线飞到购物车效果demo

Demo页面采用的是某猫某商品页面。原本的加入购物车效果也是很精致的——移动到购物车上（直线），然后落下（含高度变化）。//zxx: 您可以自己打开一个商品详细页感受下。

这里，则改成了抛物线效果。

点击demo两个“加入购物车”按钮，就可以看到抛物线落下的效果了。

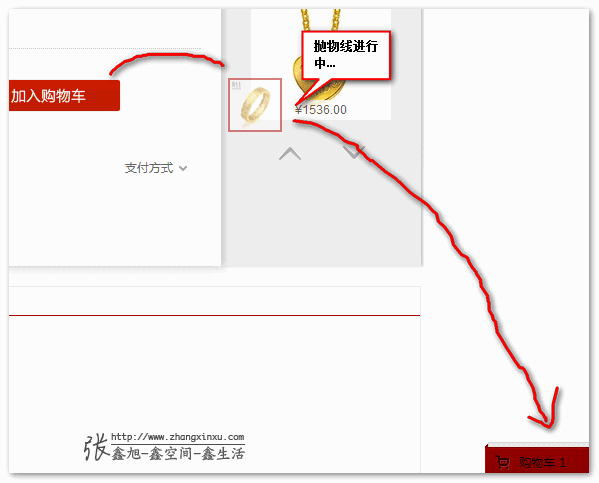
面向实际使用，实际上需要更多的细节处理。例如，接近购物车的时候，购物车是否应该有动作。进入购物车，购物车是否需要抖一下，表示我吃进去商品了，我很得瑟！等~

七、其他函数

举一反三，触类旁通。如果你想实现其他的运动轨迹效果，例如，双曲线，或者椭圆运动。都是可以借助数学函数，按照上面抛物线实现的思路。稍微折腾折腾，效果就会出来了。

这些其实都是简单的动画效果。您可能会觉得作用有限。实际上，您所见过的很多炫得掉渣子的效果都是由这个基本动画效果演变或叠加出来的。如何个演变以及叠加，这是需要技巧的。这又属于另外一个方向的知识了。

如果您对动画相关的诸多算法或技巧很在行，您也可以成为很多企业抢手的香饽饽。

八、缓动与速度

之前有介绍过缓动的一些算法。可以让动画速度先快后慢，或者先慢后快，或者弹弹弹。虽然缓动本质上也是曲线。但是，与这里的抛物线函数曲线还是不一样的。

缓动的变量单位是时间；而这里抛物线效果的变量单位是像素。

因此，缓动改变的是速度；这里改变的则是运动轨迹。

但是，相同的是，他们绘制的曲线的模样可以是类似的。也就是，他们都用到了数学。

小时候，老师的嘴巴里经常会蹦出这么句话：“学好数理化，走遍天下都不怕！”

现在明白，真的是很有道理的哈！

实际上，更有道理的是后面半句：“除非你有一个好爸爸！”

太深刻了！

九、贝塞尔曲线与任意轨迹

对于有规律的轨迹，我们可以套用数学函数。如果是没有规律的呢？比方说，我想让汽车像喝醉了酒一样曲线运动，怎么办？

可能就需要借助贝塞尔曲线绘制了。

借助SVG或者canvas.

要说SVG和canvas……

额~~一瞬间，我的大脑像高速服务区的大便池一样堵住了，这SVG以及canvas相关知识点超多，实属超大话题为避免营养过盛，消化不良，相关内容后面一点一点和大家分享。

本文至此为止，感谢大家能够阅读至此！

一般而言，搓文后面会是大作，尽请期待！

欢迎交流！

本文为原创文章，会经常更新知识点以及修正一些错误，因此转载请保留原出处，方便溯源，避免陈旧错误知识的误导，同时有更好的阅读体验。
本文地址：http://www.zhangxinxu.com/wordpress/?p=3855

（本篇完）