这篇文章发布于 2013年01月5日,星期六,21:40,归类于 外文翻译。 阅读 66534 次, 今日 2 次 12 条评论
by zhangxinxu from http://www.zhangxinxu.com
本文地址:http://www.zhangxinxu.com/wordpress/?p=2904
//zxx: 以下为翻译全文————–
数周前,我碰巧读到 Chris Coyer一篇关于边框半径嵌套的文章,这触发了我之前一直想做相关研究的蠢蠢欲动的心。
下图中,那个按钮比较正点?你是否曾经有意或无意要设计这样一个按钮,一个圆角矩形嵌套在另外一个圆角矩形中,然后你不知道应该怎么根据给定的外部半径设置内部半径大小,或者反过来根据内部半径大小设置外部大小?这就是我们接下来要探讨的。
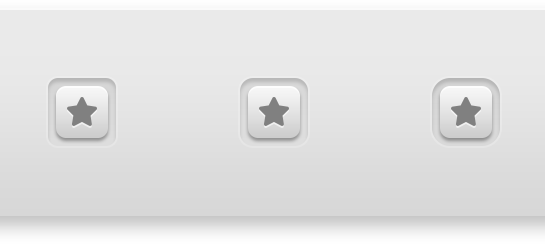
创建圆角矩形的四种方式
假设,你需要需要去创建一个内陷的按钮,你可以这样,
- 使用看上去靠谱的半径
- 内外圆角矩形使用相同的半径
- 复制外面的矩形并自由变换创建它
- 设置内径大小为外径大小再减去边框宽度
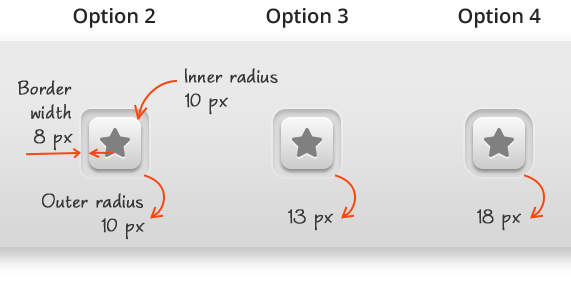
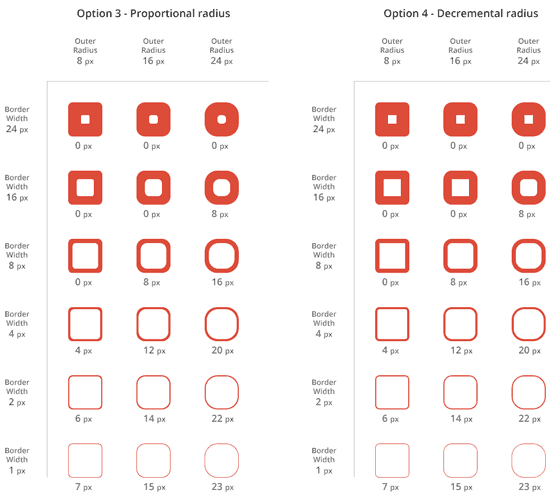
选择哪种方式
因为轻信我们的眼睛,我们不会指望选项1。从上图看来,显然选项2没什么效果。选项3和选项4看上去算是那么回事,我来在他们之中选择一个合适的~
- 对于外矩形,我选择宽度1,外半径3,边框宽度6,并在PhotoShop图层中花了18个矩形。
- 对于内矩形,两种处理,一是复制外矩形进行自由变换(选项3);二是内描边大小相等的边框宽度(选项4)。
- 坐等结果
就是你了,选项4
上面结果清楚地表明,选项4对于所有边框宽度(从1像素到24像素)都表现不错。从Photoshop判断看,也是该结果。因此,公式很简单:内半径=外半径-边框宽度。
研究继续
研究byebye了?恩,一部分吧,不是全部。你有没有注意到这种情况,当边框宽度大于等于外半径时候,内半径就是0,且按钮就是个简单的尖锐的方形?这好看吗?可以改善吗?如果有略微圆润的边角,岂不是会更好看?
进入下一阶段的学习。在机械工程中,这个圆形部分被称作为“圆角(fillet)”,通过机器操作生成这个圆角曲线称之为“角隅填密法(filleting)”(我有机械工程的学士学位:))。在我们这个例子中,角隅填密法会不会让设计更好呢?如果是这样的话,我们应该如何计算应该的圆角半径呢?
边角填充提高设计
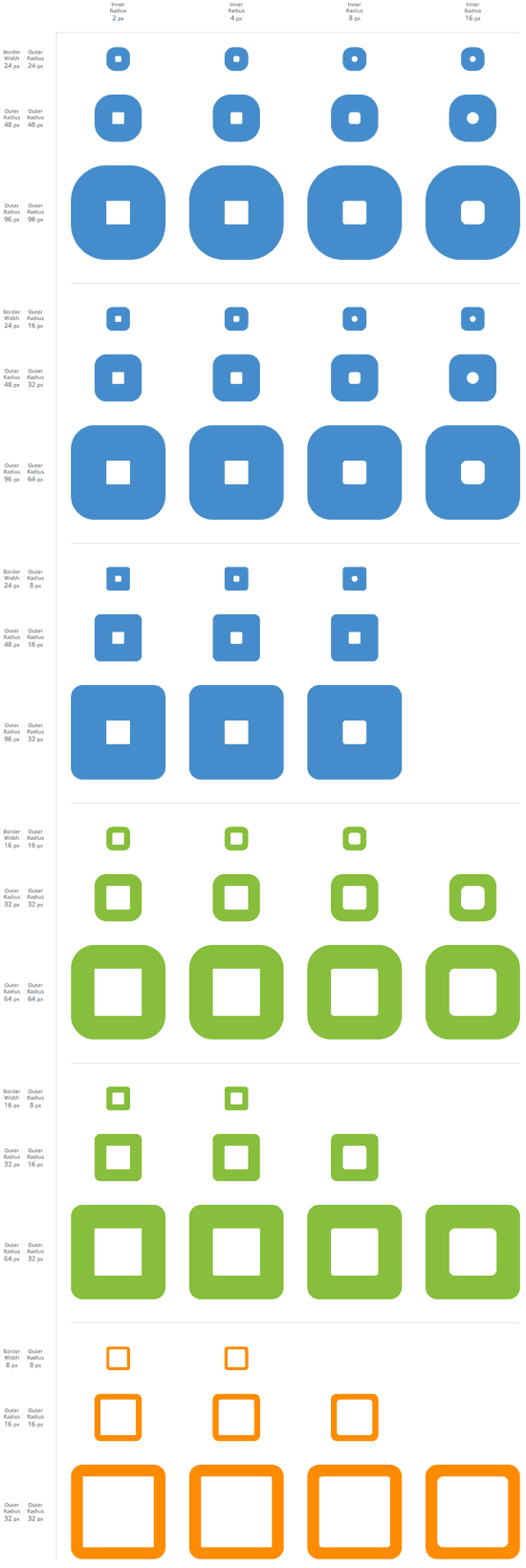
为了确认filleting可以提高设计,我选择了下面这些方形的情况,并切出了2, 4, 6以及8像素的圆角半径。下面这个表显示了结果。您可以发现,通过特定大小的圆角半径填塞,设计确实好看些了。
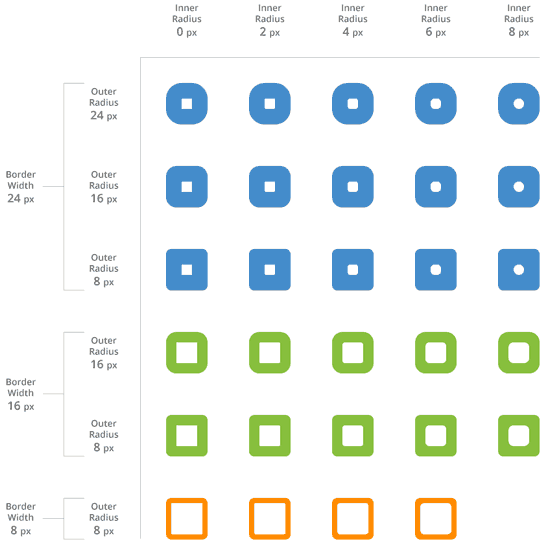
我想看看,是否半径在小尺寸有用,大尺寸也有用。所以,我就增加了一倍和四倍按钮,结果罗列入表。最好看的圆角半径貌似随着按钮大小而增加。
圆角半径的公式是什么
我试图去需找是否有确定最佳圆角半径的公式。这有可能吗?答案是Yes, 如果你给我2刀,我将来给你4刀,你给我6刀我还你12刀,给我25刀我给你50刀,那你可以轻易知道公式。从数学上讲,你可以通过将数据(2-4, 6-12, 25-50)绘制成在图表上的点,然后找到连接这些数据点的直线或曲线的公式,这个过程被称为曲线拟合。
该选择哪些数据对呢?其中一个是圆角半径;圆角半径在我看来是最好的(这不科学,我知道,但是那不属于我们现在的范围)。那另外一个呢?看上去像外半径,但谁知道呢,甚至边框宽度都能扮演一个角色。所以我绘制了两个图表,一个是找出(最佳)内半径是如何随着外半径变化的,另外一个是找出内半径是如何随着边框半径变化的。下面就是图表。注意:如果你通过选择最佳圆角半径重复该实验,结果可能不一样,因为在某些情况下,并不清楚哪个圆角半径是最佳的,因此,您就会选择相邻的圆角半径。
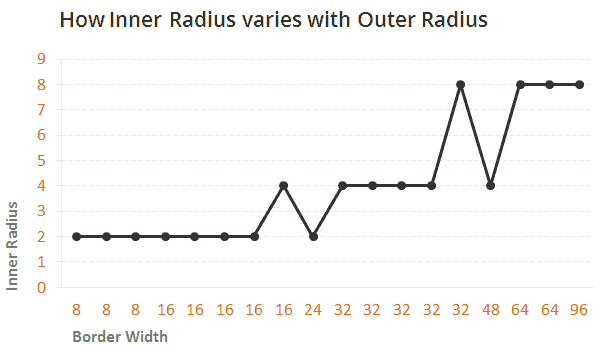
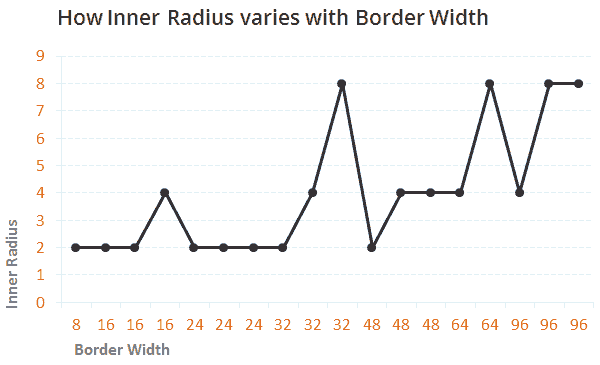
内半径的增加似乎既跟外半径又跟边框宽度同步,但不是很流畅。据我所知,只有当曲线遵循模式的时候,曲线拟合可以产生有意义的公式。该模式既可以是一条直线,抛物线,正弦波等。但是,我怀疑它是否有规律,绘制的曲线实在是太锯齿状了。
我基于自己生锈的数学知识做了整个实验。我可能错过了一些东西,或者我绘制的点不是足够的多,如果谁更加见多识广做了这个实验,绘制了更多的点,我很乐意看到结果。到目前为止,毕竟我们必须依靠我们的眼睛找到最好的圆角半径。我不入地狱谁入地狱。圆角半径公式正在躲猫猫。
总结
下次你想创建内嵌圆角矩形,遵循下面要求会有最佳结果:
- 内半径=外半径-边框宽度
- 如果内半径为0,圆角之。通过目测找到最好的圆角半径(基本上,外半径小于100像素,最佳圆角半径是1-15像素中任意位置)
//zxx: 以上为翻译全文————–
译者结语
上面内容是不是有不知所云的感觉,确实,但这也是理所当然的。一些拓荒者,希望身体力行尝试些新的东西,这些东西的成果往往都是纯粹的实验结果,或者总结的可能并不准确的理论。对于实用主义者而言,这些似乎是很枯燥的。
还有一类人属于实践者,他们总敏锐捕捉到一些新颖的理论或实验结果,然后尝试性地应用在实践中。可能这些实践并不完美,也有可能成为了该方法的创造者。
还有一类人属于求知者,时刻关注新技术的发展与脉动,于是他们成为了一些新方法飞推广者。
还有一类人属于跟风者,这个技术大牛或某大网站使用了,于是,不假思索地,葫芦画瓢地也应用上了,于是,成就了所谓的流行技术。
本文译文内容,可能原本是针对网页设计师而言,如何在Photoshop中把握内外圆角的大小,以实现最佳的内外圆角矩形嵌套效果。但是理论这东西往往是相通的,于是,我们在实现网页一些UI效果的时候,也可以应用文章所述的结论,例如:
1. 内半径=外半径-边框宽度
如下测试代码(内borderRadius = 外borderRadius – padding值 → 10=30-20):
.radius1{width:200px; padding:20px; background:#a0b3d6; border-radius:30px;}
.radius1_in{height:200px; background:#fff; border-radius:10px; }
<div class="radius1"><div class="radius1_in"></div></div>
效果如下(现代浏览器,如果您看不到效果,可能是在RSS或是其他网站查看,原文地址:http://www.zhangxinxu.com/wordpress/?p=2904):
1. 内半径<0 ,边框40宽度像素对照上面的图表,估计4像素内半径
如下测试代码:
.radius2{width:160px; border-radius:30px; border:40px solid #a0b3d6; background:#a0b3d6;}
.radius2_in{height:160px; background:#fff; border-radius:4px;}
<div class="radius2"><div class="radius2_in"></div></div>
于是,就有了最佳内外圆角大小。
本文为原创翻译,转载请注明来自张鑫旭-鑫空间-鑫生活[http://www.zhangxinxu.com]
本文地址:http://www.zhangxinxu.com/wordpress/?p=2904
(本篇完)
- CSS border三角、圆角图形生成技术简介 (0.852)
- 妙法攻略:渐变虚框及边框滚动动画的纯CSS实现 (0.611)
- 666,看hr标签实现分隔线如何玩出花 (0.594)
- 拾人牙慧 - CSS3实现Opera浏览器的logo (0.406)
- 纯CSS实现各类气球泡泡对话框效果 (0.258)
- CSS "渐进增强"在web制作中常见应用举例 (0.258)
- CSS3模拟window7炫酷界面效果展示 (0.258)
- PIE使IE支持CSS3圆角盒阴影与渐变渲染 (0.258)
- 需警惕CSS3属性的书写顺序 (0.258)
- 小tip:CSS3下的圆形遮罩效果实现与应用 (0.258)
- CSS3选择器:nth-child和:nth-of-type之间的差异 (RANDOM - 0.018)

光这个标题,就会吸引好多处女座来围观
如果外半径不是是质数, 内半径是外半径因子集合S(不包含自身然后再去掉最大的。)
css没有inner-radius这个属性呢
一向这么做,一向以为要做个同心圆实现一个等壁厚。一向没想这么多。
@紫 可以试试pie.htc文件。
可是border-radius这个属性只有google和FF支持,IE9以下都是不支持的啊,如何可以让在IE中也能支持啊
@张 鑫旭 无情者伤人,有情者自伤。
圆角也可以这么深入,很喜欢
大哥你网站被攻击了吧
@z 外链太多,自损八百可伤敌一千~
研究的很深入啊,赞!
以前ps的时候一直选择圆角一样大的,总觉得有问题,现在又了答案。谢谢。