这篇文章发布于 2012年06月8日,星期五,01:16,归类于 CSS相关。 阅读 649863 次, 今日 35 次 193 条评论
by zhangxinxu from http://www.zhangxinxu.com
本文地址:http://www.zhangxinxu.com/wordpress/?p=2427
一、哥,我被你吓住了
打架的时候会被块头大的吓住,学习的时候会被奇怪名字吓住(如“拉普拉斯不等式”)。这与情感化设计本质一致:界面设计好会让人觉得这个软件好用!
所以,当看到上面“Matrix(矩阵)”的时候,难免会心生畏惧(即使你已经学过),正常心理。实际上,这玩意确实有点复杂。
然而,这却是屌丝逆袭的一个好机会。
CSS同行间:
你是不是有这样的感觉:哎呀呀,每天就是对着设计图切页面,貌似技术没有得到实质性地提升啊,或者觉得日后高度有限!
我们应该都知道二八法则(巴莱多定律),即任何一组东西中,最重要的只占其中一小部分,约20%,其余80%的尽管是多数,却是次要的。如果你有上述的感觉,那你就属于那80%, 一抓一大把,没有特色的页面仔。
CSS门槛低,无需程序基础或数学逻辑能力,也能做出点自我感觉不错的东西。然而,你自己也应该清楚的,一般你能轻松学到的东西,别人也可以。因此,如果你想挤进那20%的行列,就要学到一般人学不到的深度,学到一般人学不了的东西。自然,是需要更多额外的努力的。如果每次你都比别人努力一点点,何愁不比他人高出几等。人年轻的时候,贵在坚持!
而这里的CSS矩阵就是展现你与其他芸芸同行差异的好契机。很多人看到名字就畏惧了,看到奇怪的数学书写就吓退了;而你没有,迎难而上,把摇手机的时间用在理解矩阵上。自然,你就冒尖了一点。类似的,很多其他CSS方面的东西,你也比别人多深入学习一点,怎么可能就是个普通的页面仔呢?
因此,从这里开始,摆脱那80%的行列吧!
伪同行间:
虽然都是从事计算机,虽然都是从事互联网,虽然都是写代码的,(据说)写JAVA的瞧不起写JavaScript的,写JavaScript的瞧不起写CSS的。这可以理解,虽然养鸡养鸭成为富翁的不在少数,但是,一说你是农村养鸡的,怎么样?上海专业的丈母娘们的视线立马下降60°——被BS了。倒不是因为你是干农业的,而是“鸡”的问题;如果说你是饲养斯里兰卡蓝孔雀的,得,挑剔的丈母娘们说不定就会正脸看看(唷,斯里兰卡,国外货;唷,孔雀,高档货)。
同样的,如果你掌握的CSS都是些“砌砖头”的活(虽然砌砖头也是大学问),被无视也情理之中。但是,矩阵这个东西,就是扭转乾坤(网称“逆袭”)的好东西:CSS中也是有复杂的高档货的。再忽悠些“图形算法、位置计算”之类的词句,嘿嘿,立马看法从 变成
变成 。
。
二、何为矩阵?
矩阵可以理解为方阵,只不过,平时方阵里面站的是人,矩阵中是数值:
 →
→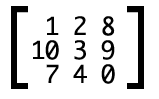
而所谓矩阵的计算,就是两个方阵的人(可以想象成古代的方阵士兵)相互冲杀。
CSS3中的矩阵
CSS3中的矩阵指的是一个方法,书写为matrix()和matrix3d(),前者是元素2D平面的移动变换(transform),后者则是3D变换。2D变换矩阵为3*3, 如上面矩阵示意图;3D变换则是4*4的矩阵。
有些迷糊?恩,我也觉得上面讲述有些不合时宜。那好,我们先看看其他东西,层层渐进——transform属性。
具体关于transform属性具体内容可以点击这里补个课。稍微熟悉的人都知道,transform中有这么几个属性方法:
.trans_skew { transform: skew(35deg); }
.trans_scale { transform:scale(1, 0.5); }
.trans_rotate { transform:rotate(45deg); }
.trans_translate { transform:translate(10px, 20px); }
斜拉(skew),缩放(scale),旋转(rotate)以及位移(translate)。
那你有没有想过,为什么transform:rotate(45deg);会让元素旋转45°, 其后面运作的机理是什么呢?
下面这张图可以解释上面的疑问:
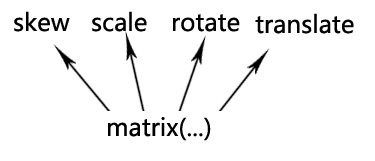
无论是旋转还是拉伸什么的,本质上都是应用的matrix()方法实现的(修改matrix()方法固定几个值),只是类似于transform:rotate这种表现形式,我们更容易理解,记忆与上手。
换句话说,理解transform中matrix()矩阵方法有利于透彻理解CSS3的transform属性,这就与那80%的也会应用但只知表象的人拉开了差距!
OK,现在上面提到的CSS3矩阵解释应该说得通了。
三、矩阵应用场景
虽然题目写的是“transform中的Matrix”,实际上,在CSS3以及HTML5的世界里,这玩意还是涉猎蛮广的,如SVG以及canvas.
事实上,关于矩阵,我之前曾经介绍过,是在介绍IE浏览器下的Matrix矩阵滤镜的时候说过,IE的滤镜矩阵与CSS中的矩阵虽然写法上差异较大,但是,矩阵计算的原来是一致的。只是之前的介绍主要是IE下的旋转与缩放,同时也不是很深入,因此还有有些局限的。
四、transform与坐标系统
用过transform旋转的人可以发现了,其默认是绕着中心点旋转的,而这个中心点就是transform-origin属性对应的点,也是所有矩阵计算的一个重要依据点(下图参考自dev.opera.com)。
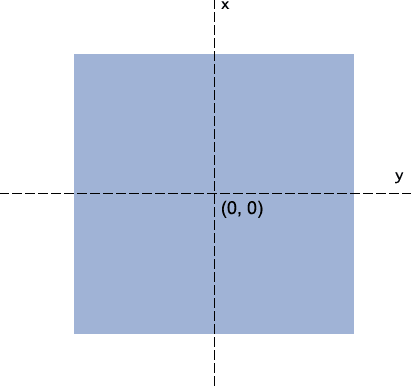
当我们通过transform-origin属性进行设置的时候,矩阵相关计算也随之发生改变。反应到实际图形效果上就是,旋转拉伸的中心点变了!
举例来说,如果偶们设置:
-webkit-transform-origin: bottom left;
则,坐标中心点就是左下角位置。于是动画(例如图片收缩)就是基于图片的左下角这一点了:
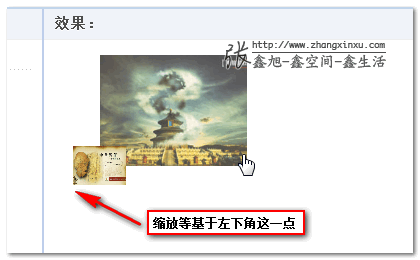
上图效果可以点击这里查看(Chrome浏览器)。
再举个稍微难理解的例子,我们如果这样设置:
transform-origin: 50px 70px;
则,中心点位置有中间移到了距离左侧50像素,顶部70像素的地方(参见下图),而此时的(30, 30)的坐标为白点所示的位置(这个位置后面会用到)。
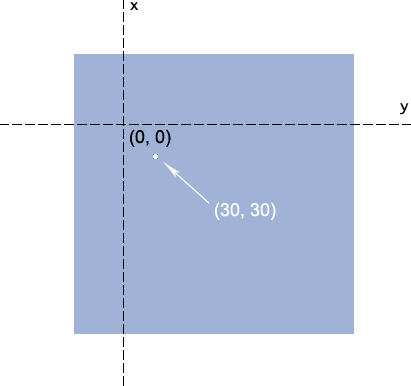
仔细看看,是不是很快就理解了哈~~
五、准备好了没?重头戏来了
CSS3 transform的matrix()方法写法如下:
transform: matrix(a,b,c,d,e,f);
吓住了吧,这多参数,一个巴掌都数不过来。好吧,如果你把a~f这6个参数想象成女神的名词,你会觉得,世界不过如此嘛~~
实际上,这6参数,对应的矩阵就是:
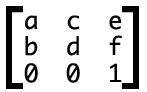
注意书写方向是竖着的。
上面提过,矩阵可以想象成古代的士兵方阵,要让其发生变化,只有与另外一个士兵阵火拼就可以了,即使这是个小阵。
反应在这里就是如下转换公式:
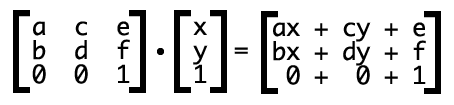
其中,x, y表示转换元素的所有坐标(变量)了。那后面的ax+cy+e怎么来的呢?
//zxx:大学时候线性代数知识,懂的人这里可以直接跳过
很简单,3*3矩阵每一行的第1个值与后面1*3的第1个值相乘,第2个值与第2个相乘,第3个与第3个,然后相加,如下图同色标注:
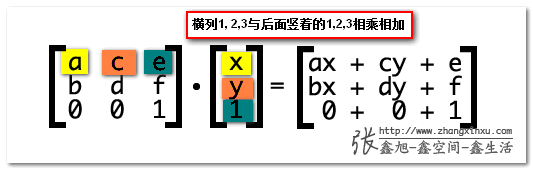
那ax+cy+e的意义是什么?
记住了,ax+cy+e为变换后的水平坐标,bx+dy+f表示变换后的垂直位置。
又迷糊了?不急,一个简单例子就明白了。
假设矩阵参数如下:
transform: matrix(1, 0, 0, 1, 30, 30); /* a=1, b=0, c=0, d=1, e=30, f=30 */
现在,我们根据这个矩阵偏移元素的中心点,假设是(0, 0),即x=0, y=0。
于是,变换后的x坐标就是ax+cy+e = 1*0+0*0+30 =30, y坐标就是bx+dy+f = 0*0+1*0+30 =30.
于是,中心点坐标从(0, 0)变成了→(30, 30)。对照上面有个(30, 30)的白点图,好好想象下,原来(0,0)的位置,移到了白点的(30, 30)处,怎么样,是不是往右下方同时偏移了30像素哈!!
实际上transform: matrix(1, 0, 0, 1, 30, 30);就等同于transform: translate(30px, 30px);. 注意:translate, rotate等方法都是需要单位的,而matrix方法e, f参数的单位可以省略。
一例胜万语,您可以狠狠地点击这里:matrix(1,0,0,1,30,30)实例demo
在现代浏览器下,会有类似下面动图的效果:

效果只是表象的,我想到了一个更好的idea去表现矩阵到底是如何变换的,您可以狠狠地点击这里:matrix分解变换演示
为了提高性能,demo中每个单元分解成了5px * 5px的区域。演示分两步,先是演示每个单元的位置是如何计算的,接着动画表现其位置的偏移。
这个demo所做的工作就是把浏览器瞬间完成的计算和渲染变成了可控的分步显示,这样,大家就可以很直观地看出,这个矩阵计算到底是如何起作用的。下图为正在演示过程中的截图:
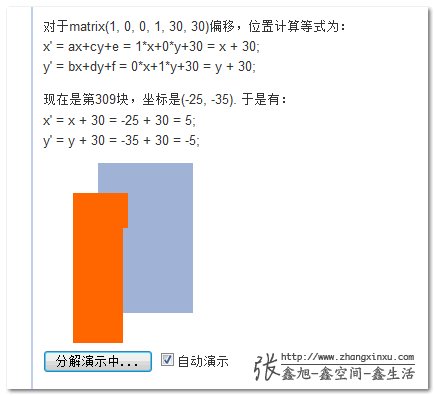
//zxx:由于默认100毫秒间隔不断渲染,因此如果你电脑CPU或是浏览器hold不住,可以取消“自动演示”的勾选,然后,点击左边的按钮手动分步查看。
总结
聪明的你可能以及意识到了,尼玛matrix表现偏移就是:
transform: matrix(与我无关, 哪位, 怎么不去高考, 打麻将去吧,水平偏移距离, 垂直偏移距离);
你只要关心后面两个参数就可以了,至于前面4个参数,是牛是马,是男是女都没有关系的。
六、transform matrix矩阵与缩放,旋转以及拉伸
偏移是matrix效果中最简单,最容易理解的,因此,上面很详尽地对此进行展开说明。下面,为了进一步加深对matrix的理解,会简单讲下matrix矩阵与缩放,旋转以及拉伸效果。
缩放(scale)
上面的偏移只要关心最后两个参数,这个缩放也是只要关心两个参数。哪两个呢?
如果你足够明察秋毫,应该已经知道了,因为上面多次出现的:
transform: matrix(1, 0, 0, 1, 30, 30);
已经出卖了。
发现没,matrix(1, 0, 0, 1, 的元素比例与原来一样,1:1, 而这几个参数中,有两个30, 30);1, 啊哈哈!没错,这两个1就是缩放相关的参数。
其中,第一个缩放x轴,第二个缩放y轴。
用公式就很明白了,假设比例是s,则有matrix(s, 0, 0, s, 0, 0);,于是,套用公式,就有:
x' = ax+cy+e = s*x+0*y+0 = s*x;
y' = bx+dy+f = 0*x+s*y+0 = s*y;
也就是matrix(sx, 0, 0, sy, 0, 0);,等同于scale(sx, sy);
好了,至此,无需多说了……
眼见为实,因此demo还是要滴,您可以狠狠地点击这里:matrix矩阵与缩放demo
为了避免元素比例放大时候遮盖上面的文本框以及描述位子,因此,将元素的坐标原点迁至了左上角。

旋转(rotate)
旋转相比前面两个要更高级些,要用到(可能勾起学生时代阴影的)三角函数。
方法以及参数使用如下(假设角度为θ):
matrix(cosθ,sinθ,-sinθ,cosθ,0,0)
结合矩阵公式,就有:
x' = x*cosθ-y*sinθ+0 = x*cosθ-y*sinθ y' = x*sinθ+y*cosθ+0 = x*sinθ+y*cosθ
这个与IEMatrix滤镜中的旋转是有些类似的(M11表示矩阵第1行第1个(参数a),M21表示矩阵第2行第一个(参数b)……):
filter:progid:DXImageTransform.Microsoft.Matrix(M11=cosθ,M21=sinθ,M12=-sinθ,M22=cosθ');
哎呀呀,四个参数,我记不住啊!莫慌,我们可以这样子记忆:
CS-SC:初三-上床,对称结构,这下忘不了了吧~~
您可以狠狠地点击这里:transform matrix矩阵与旋转demo

不过,说句老实话,就旋转而言,rotate(θdeg)这种书写形式要比matrix简单多了,首先记忆简单,其次,无需计算。例如,旋转30°,前者直接:
transform:rotate(30deg);
而使用matrix表示则还要计算cos, sin值:
transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);
拉伸(skew)
拉伸也用到了三角函数,不过是tanθ,而且,其至于b, c两个参数相关,书写如下(注意y轴倾斜角度在前):
matrix(1,tan(θy),tan(θx),1,0,0)
套用矩阵公式计算结果为:
x' = x+y*tan(θx)+0 = x+y*tan(θx) y' = x*tan(θy)+y+0 = x*tan(θy)+y
对应于skew(θx + "deg",θy+ "deg")这种写法。
其中,θx表示x轴倾斜的角度,θy表示y轴,两者并无关联。
还是靠实例说话吧,您可以狠狠地点击这里:matrix矩阵与拉伸demo
在Chrome下可以很动态地查看不同倾斜角度对应的拉伸的效果:

七、既然有简单的skew, rotate..,那matrix有何用?
我想有人会奇怪,既然CSS3 transform中提供了像skew, rotate, …效果,那还需要掌握和熟悉让人头大的矩阵方法干嘛呢?
好问题,确实,对于一般地交互应用,transform属性默认提供的些方法是足够了,但是,一些其他的效果,如果transform属性没有提供接口方法,那你又该怎么办呢?比方说,“镜像对称效果”!
没辙了吧,这是,就只能靠matrix矩阵了。要知道,matrix矩阵是transform变换的基础,可以应付很多高端的效果,算是一种高级应用技巧吧。掌握了基础,才能兵来将挡水来土掩啊。
OK,这里就演示下,如何使用CSS3 transform matrix矩阵实现镜像效果。
这个有点难度,因此,我们先看demo,您可以狠狠地点击这里:matrix与镜像对称效果demo
框框中输入旋转的角度值(用来确定镜像的对称轴),然后失去焦点,就会呈现出对应的镜像对称效果了:
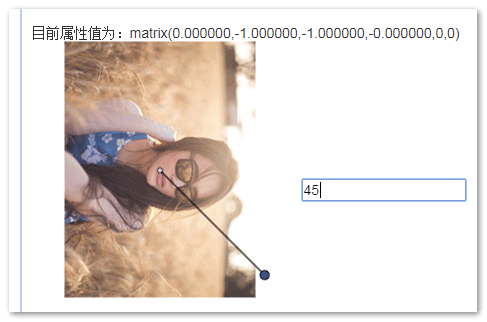
您可以在FireFox或是Chrome等浏览器上体验下matrix实现的镜像渐变效果。
demo页面中的一个轴是为了便于理解我加上的效果,实际上,在镜像对称的时候轴是看不见的。
轴围绕的那个点就是CSS3中transform变换的中心点,自然,镜像对称也不例外。因为该轴永远经过原点,因此,任意对称轴都可以用y = k * x表示。则matrix表示就是:
matrix((1-k*k) / (1+k*k), 2k / (1 + k*k), 2k / (1 + k*k), (k*k - 1) / (1+k*k), 0, 0)
这个如何得到的呢?
啊,高中数学来了,就当再高考一次吧,如下图,已经y=kx,并且知道点(x, y)坐标,求其对称点(x’, y’)的坐标?
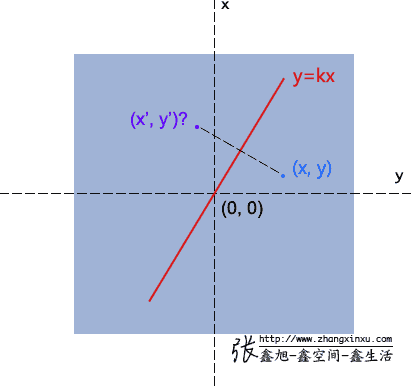
很简单,一是垂直,二是中心点在轴线上,因此有:
(y-y') / (x - x') = -1/ k → ky-ky' = -x+x'
(x + x') / 2 * k = (y + y')/2 → kx+kx' = y+y'
很简单的,把x'和y'提出来,就有:
x' = (1-k*k)/(k*k+1) *x + 2k/(k*k+1) *y;
y' = 2k/(k*k+1) *x + (k*k-1)/(k*k+1) *y;
再结合矩阵公式:
x' = ax+cy+e;
y' = bx+dy+f;
我们就可以得到:
a = (1-k*k)/(k*k+1);
b = 2k/(k*k+1);
c = 2k/(k*k+1);
d = (k*k-1)/(k*k+1);
也就是上面matrix方法中的参数值啦!
下图为自己计算的草稿:

八、3D变换中的矩阵
3D变换虽然只比2D多了一个D,但是复杂程度不只多了一个。从二维到三维,是从4到9;而在矩阵里头是从3*3变成4*4, 9到16了。
其实,本质上很多东西都与2D一致的,只是复杂度不一样而已。这里就举一个简单的3D缩放变换的例子。
对于3D缩放效果,其矩阵如下:
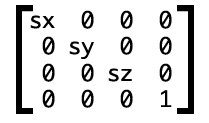
代码表示就是:
transform: matrix3d(sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1)
您可以狠狠地点击这里:matrix3d下的3D比例变换demo
补充于2013-04-24
关于3D变换,可以参见邪恶的这篇文章:“CSS3 3D transform变换,不过如此!”
九、结束语
想了想,没什么要唠叨的。文中观点若是存在疑问或不准确的,欢迎指正。感谢阅读!
参考文章:
Understanding the CSS Transforms Matrix
CSS3前端开发中需要用到的变换矩阵
本文为原创文章,转载请注明来自张鑫旭-鑫空间-鑫生活[http://www.zhangxinxu.com]
本文地址:http://www.zhangxinxu.com/wordpress/?p=2427
(本篇完)
- 小tip: IE下zoom或Matrix矩阵滤镜中心点变换实现 (0.581)
- IE矩阵滤镜Matrix旋转与缩放及结合transform的拓展 (0.505)
- 借助SVG文字尺寸自动缩放甚至突破Chrome 12px限制 (0.417)
- JS之我用单img元素实现了图像resize拉伸效果 (0.417)
- 趁热打铁,SVG feColorMatrix滤镜gogogo! (0.371)
- 了不起的IE7浏览器-CSS新特性-实现与思维变革 (0.232)
- 理解SVG transform坐标变换 (0.210)
- 小tips: 在canvas上实现元素图片镜像翻转动画效果 (0.210)
- Pixi.js中ColorMatrixFilter自带滤镜效果一览 (0.185)
- CSS3+js实现多彩炫酷旋转圆环时钟效果 (0.134)
- 借助CSS Shapes实现元素滚动自动环绕iPhone X的刘海 (RANDOM - 0.007)

要不要这么喜欢张含韵。。。
关于rotate旋转的公式证明
当前坐标x,y,相对x角度a,转为极坐标(r(x^2+y^2,a)),
当顺时针旋转b角度,极坐标转为(r,a-b),
极坐标转直角坐标为 x`=r*cos(a-b); y`=r*sin(a-b);
根据三角和差公式
Sin(A+B)=SinA*CosB+SinB*CosA
Sin(A-B)=SinA*CosB-SinB*CosA
Cos(A+B)=CosA*CosB-SinA*SinB
Cos(A-B)=CosA*CosB+SinA*SinB
得出x` = r*cos(a)*cos(b) + r*sin(a)*sin(b) = x*cos(b) + y*cos(b)
y` = r*sin(a)*cos(b) – r*cos(a)*sin(b) = y*cos(b) – x*sin(b)
基本上没错,符号可能有些错。。
感觉大叔把rotate那边的旋转公式搞错了?
x’ = x*cosθ-y*sinθ+0 = x*cosθ-y*sinθ
y’ = x*sinθ+y*cosθ+0 = x*sinθ+y*cosθ
这是逆时针旋转
但是好像CSS里是顺时针旋转的
那就要把角度换成负值代入了
具体没试 已经有点晕 要休息下….哈哈哈哈
哦 笛卡尔坐标… Y轴朝下… 所以我指正错了…
旋转这里matrix(a,b,c,d,e,f)这里有点不明白,没得上面最开始的偏移,缩放讲的细致,一下就出来了,自己整了半天没搞明白,可能也和很久没碰三角函数有关吧。
旋转的具体可以看这篇
【旋转坐标转换的矩阵推导】
http://www.cnblogs.com/yuzhongwusan/p/4121815.html
需要注意的是css 的y轴是向下的。所以得出的公式符号会有不同,不过最终结果是一样的。
斜拉(skew),缩放(scale),旋转(rotate)以及位移(translate)
matrix(ScaleX,SkewY,SkewX,ScaleY,OffX,OffY)
这些都理解了,但是旋转部分理解不了,只理解了简单旋转
如果先有斜拉,缩放,旋转,位移操作在旋转,就不会计算了
用JS写了个matrix代码生成器,斜拉(skew),缩放(scale),旋转(rotate)以及位移(translate)功能都实现了,但是先有斜拉,缩放,旋转,位移操作在旋转就搞不定了,
大婶出个生成器呗
例子都是基于matrix(1, 0, 0, 1, 0, 0);的理想初始值
假设:
缩放(scale) X=2,Y=3
斜拉(skew) X=30deg Y=60deg
Math.tan(60 * Math.PI / 180)=0.577350
Math.tan(30 * Math.PI / 180)=1.732051
位移(translate) X=10 Y=20
旋转(rotate) 45deg
不考虑旋转结果应该是
matrix(2, 1.732051,0.577350, 3, 10, 20);
旋转角度这么代入计算??
对呀 同时出现 缩放,位移,旋转 怎么计算??
transform: matrix(1, 0, 0, 1, 30, 30);就等同于transform: translate(30px, 30px);
transform:matrix(sx, 0, 0, sy, 0, 0);,等同于scale(sx, sy);
单独的一个属性用一个矩阵的我能看懂,那如果斜拉(skew),缩放(scale),旋转(rotate)以及位移(translate)一块发生变化,那用矩阵怎么表示的呢 ?
css图解上和你说的一样,但是上边也没说这几个属性和到一块是怎么用矩阵表示的,求指点
这个有两种做法,一、你逐步做matrix变换 二、逐步变换很麻烦,则算出每一种变换的矩阵,按照变换的顺序进行相乘,得到最终的matrix,然后设置css即可
你说的相乘是什么规则相乘呢?就下边的例子来说
transform: matrix(1, 0, 0, 1, 30, 30);就等同于transform: translate(30px, 30px);
transform:matrix(sx, 0, 0, sy, 0, 0);,等同于scale(sx, sy);
结合到一起:transform:matrix(1*sx,0,0,1*sy,0*30,0*30);你是这意思吗
这玩意时间长了还是忘记,仍然得来这里。
其实我就想看看3D矩阵为什么是16个参数,结果没有写。2D不都省略了三个吗
我也是,结果没写
因为3d矩阵是4×4的矩阵
同时拉伸和旋转要怎么写矩阵?
如果是scale、skew、translate等这些效果一起用matric表示出来呢?
我也遇到这个问题 没有那么简单
我已经把css给的那个transform借口 在js 中全部实现了
请问是什么的接口?有相关资料吗?
x’ = ax+cy+e = s*x+0*y+0 = s*x;
y’ = bx+dy+f = 0*x+s*y+0 = s*y;
这个如果用matrix(1.5,0,0,1.5,100,100) 代入算出来的放大倍数应该是1.5X+100,1.5Y+100; 但它怎么就是放大1.5倍,向右向左移动100px?
旋转效果 270° 的时候 旋转动画效果不正确,虽然最后角度是对了。求解?
我感觉e f 的位置应该在第三行0 0 的位置,从数学上来讲的话,您是不是做了一次初等变换消元了,把 行【e f 1】变成列【e f 1】
真心请教,急急急
前端小白请教您,为什么4个变量拉伸, 旋转, 矩阵, 缩放,假设的矩阵参数是6个?transform: matrix(1, 0, 0, 1, 30, 30); 为什么是3阶矩阵?不是2阶?(因为只有x,y的坐标) 为什么矩阵要那样写? 真心求教,感谢
最近一个项目中遇到需要背景跟随鼠标位置发生角度变换,我直接使用rotateX,rotateY,在控制台中看到角度变换 而实际显示中 没有变换 鼠标停下来以后,背景才开始变化
matrix与镜像对称效果demo里面辅助的对称轴弄反了,虽然图像镜像没问题,但对称轴显示反了,45°时显示的对称轴是-45°的,怪不得看得怪怪的…..
很厉害的前端博主,数据厉害!
我后端开发经验4年,居然4年后才读到这里,可怕。。。
比我优秀的人都这么努力了,我努力还有什么用 /(ㄒoㄒ)/~~
请问matrix()在模仿rotate(720deg)这种效果时应该怎么写?cos和sin的值就是在0-360的范围内吧。
另外如果有多个transform的效果同时进行,matrix()也需要写多个么
同样的疑问
开呐。。我个高中学历也把文章看完了,不是很懂的说。哭哭,,看到这些数学公式就有点怕怕
说话的画风这么可爱,一定是个蓝孩纸~
其实2d转换用不着3×3的矩阵,2×3就够了,最下面的[0,0,1]完全没什么卵用,倒是让读者迷惑
是不是3D矩阵3×4就够了?
因为2d转换是3阶矩阵,是基于单位矩阵的!所以最下面的[0,0,1]是必须的!
这个计算对称点的方法不是很好。
虽然是个简单的问题,但是我认为还是有必要研究一下,
有个简洁的方法,我中学总结的,编程一直在使用。
(x0,y0)关于直线 Ax+By+C=0 的对称点为:
x=x0-n*A*D
y=y0-n*B*D
其中 n=2
其中D=(Ax0+By0+C)/(A*A+B*B);
特别地,n=1 为垂足,n其他值 则为这个矢量方向上的其他点。
这个式子很容易记住的。
–传说胡歌
——-有点心得,感谢你写的文章。从事前端几年,特别研究svg
没看懂,能举个实际例子吗?
看到最后,如果我们对一个图片转换的时候,只知道角度,各个转换的角度,最后那个K的斜率是怎么算出来的。希望大神指点迷津。
K就是斜率,知道旋转的角A,那么K=tanA
左下角的广告把文章挡住了,是不是可以考虑挪到右边去 ->,->
display:none;
楼主你没有详细解释每个效果中的x y分别是代表什么,如果translate的xy代表中心点坐标,scale的xy代表元素的宽高,那么下面的rotate和skew的xy都是代表什么呢
这里4种变换的x,y应该都是指元素每个像素点相对于变换原点的位置,是个变量。
最后的一个例子是旋转效果,好像不是镜像效果啊
大神啥时候写个cubic-bezier的理解课程啊,跪谢了
有的,深度掌握SVG路径path的贝塞尔曲线指令 – http://www.zhangxinxu.com/wordpress/2014/06/deep-understand-svg-path-bezier-curves-command/
本人小白。实测 matrix(0.5,0.866,0.866,-0.5,0,0);相当于scale(-1,1) rotate(120deg);。matrix算起来太麻烦了,可以分成两步来。望各路过大神指点0.0感谢感谢
我觉得您说话的风格和唐唐(任真天还是任天真)很像,你也学习他做一个前端脱口秀把这些吐槽加知识说出来,一定火!我支持你!
本来不想回复的,那个91年的小伙子 天天做视频,我曾经就有过一个疑问,他是如何面对其父母的 ,论金钱的重要性
对您表示一下膜拜之情!
讲得挺好,不过镜像变换也能用scale(-1)做到吧
●scale(-1)实现了180°镜像。
●博主的demo展现了任意角度的对称镜像。
镜像变换算错了!
请问matrix中 a b c d e f 0 0 1这个0 0 1代表什么,哪位朋友知道劳驾给说说,谢谢!
特别棒,很喜欢
讲解真的很详细,让我又预习的一遍矩阵,然后也对transform有了深刻的理解。非常感谢!
不过发现文章里面有几处比较严重的表述有误的问题,直接的结果就是把我搞糊了。比如这一类的“也就是matrix(sx, 0, 0, sy, 0, 0);,等同于scale(sx, sy);”,其实结果用matrix(sx, 0, 0, sy, 0, 0)表述是不妥的,这个矩阵的结果得到的是点(x,y)的新值,就是x’=sx,y’=sy,它等同于scale(s,s)。sx,sy其实是一个像素位置了。
我表述不好,大神见谅。
x,y默认都是1,1吗?
感觉那个镜像变换你是不是算错了。结果中没有二倍,那个2在之前已经销掉了吧?
你的网站上好多前端知识,受益非浅,非常感谢。
讲解很详细,喜欢!
镜像对称效果——也能用普通的方式实现,用-1
svg你用-1试一下就知道了
老师解释得很透彻
写了一个前端中的变换矩阵,从浏览器等角度详细解读了一下~
https://github.com/alvarto/blog/issues/1
谢谢博主的分享。你太劲了!
经常百度问题都来到博主网站~~~可见其功力十足!
12年的文章,我现在才读到,久违了
有两个问题很困扰
1.如何从一个叠加了各种transform效果的矩阵中获取其中一种变换的参数(除了translate)
2.用ele.style.webkitTransform获取样式,如果样式是写在元素内联style里的话,获取的是我们常用的”-webkit-transform:translate(XX,XX)..”字符串,如果该样式是写在css里的,获取的是矩阵matrix,难道为了容易获得某种变换的参数,(用js)把样式写成内联的比较好?
领教了
使用Matrix设置旋转360,直接回到了原点。不会有旋转的效果。
还有就是,使用旋转需要前面四个参数,这意思就是说不能同时设置旋转和缩放?
CS-SC:初三-上床
狠!!!
谢谢,终于恍然大悟了,虽然还是很复杂的,很好奇一件事,大侠的好多demo的图像都是这个姑娘啊。。。。。哈哈
博主,,
1、有没有什么方法用js直接获取到角度数啊?我用的是var m_rotate = $(“.baby_m”).css(“-moz-transform”);直接获取到的是矩阵。?
2、如果没有,那有什么方法是把矩阵转换成角度的?
3、canvas可以直接使用矩阵么?
我这个问题比较急,希望博主尽快回复啊!在此谢谢博主了。
1、没有
2、可以通过矩阵,用反正切函数换算出来弧度,然后再转换成角度即可
3、可以
不是博主,只是路过^^
LZ,我真的被你的文章感动得无言以对了,首先,在前面那么激励我们。要摆脱那80%的人,后面,文章细致琳琳,真心无法用语言说啥啊~
很详细的,点赞。
不过skew 翻译为拉伸貌似有点不妥。
变形吗
应该是斜切
叫切变更合适吧,
ps里好像叫斜切,不过我喜欢叫“歪斜”